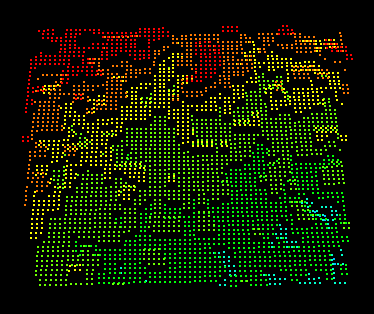
I’m working on a project to monitor trailer loading using 3D sensors. The data is really interesting and somewhat challenging. PrimeSense has some amazing technology for low-cost depth sensing. But at large distances (and possibly because of reflections and our unique geometry), quantization and other errors give examples like below. This image is looking head-on at a flat wall, but the point cloud is anything but flat. The points are spread out over a few feet in sheets perpendicular to the camera sensing axis.

To make sure we’re not developing algorithms “tuned” to this specific error model, I wanted to generate some “truth” point clouds as references. I ran across a couple different ways to do this, including ROS Gazebo plugins. But they all required building a world model which seemed quite a bit of effort for my simple case. So I spent some time to make a simulator that lets me generate point clouds during an idealized loading process. It runs so fast that I can generate a separate point cloud for each loaded package. A whole load profile consists of hundreds of point clouds, but only takes a few seconds to generate.

In general, the problem we need to solve is to find the distance from the camera to the trailer wall or package surfaces. The general equation for this distance is

where $\textbf{p}$ is a point on the plane, $\textbf{n}$ is the normal to the plane, $\textbf{c}$ is the camera location and $\textbf{u}$ is the unit vector of the ray coming out of the camera that we want to measure depth along.

The first way to simplify the problem is to use boxes (rectangular cuboids), for our package shapes and trailer shape. We then pick a specific coordinate system to simplify the distance computations. By picking the camera as the origin and axes aligned with the box surface normals, the distance computation simplifies to

where the $i$th element is the vector component along the corresponding coordinate axis.

We have two different cases to compute. In the one case, the camera is outside of the box of interest (we’re computing the distance to a package) and we want to use the external surface normals. In the other case, the camera is inside the box (we’re computing the distance to the trailer wall) and we want to use the internal surface normals.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

enum class Normal {INTERIOR, EXTERIOR};

bool
Face::does_intersect_ray_with_normal(Vector3 const& u, Normal normal) const {
  Length projection = surface_ * u[axis_];
  if (normal == Normal::EXTERIOR) {
    // test the direction opposite the normal of the surface
    projection = - projection;
  }
  return projection > 0;
}

Length
Box::distance_to_plane_along_ray(Face const& face, Normal normal, Vector3 const& u) const {
  return face.does_intersect_ray_with_normal(u, normal) ?
    face_coordinate(face) / u[face.axis()] : Limits::infinity();
}

So we simplify the distance computation, but then we also reduce the number of distance calculations needed to generate each point cloud. Instead of modeling all the packages in the trailer, we only model one stack of packages that fills the cross-sectional area of the trailer. We then walk this stack forward from the back of the trailer to the front one package at a time from left to right, bottom to top. This lets us avoid any gravity or collision calculations for placing boxes on top of others. The downside is that we’re restricted to having the same depth for all packages, but we’re still able to design a stack consisting of different frontal shapes.

Finally, to fail fast when the camera ray is not pointing near a particular package, we compute a bounding interval which encompasses the corners of the package and don’t bother with the distance calculation if the components are out of range.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Length
Box::minimum_exterior_distance_along_ray(Vector3 const& u) const {
  float min_distance = Limits::infinity();

  if (interval_.includes(u)) {
    // bottom and back faces should never be visible
    for (auto const& face : {FRONT_FACE, RIGHT_FACE, LEFT_FACE, TOP_FACE}) {
      float d = distance_to_plane_along_ray(face, Normal::EXTERIOR, u);
      if (d < min_distance) {
        Vector3 intersection = u * d;
        if (is_point_within_bounds_along_axis(intersection, face.axis())) {
          min_distance = d;
        }
      }
    }
  }
  return min_distance;
}

Now we can generate point clouds like the following.

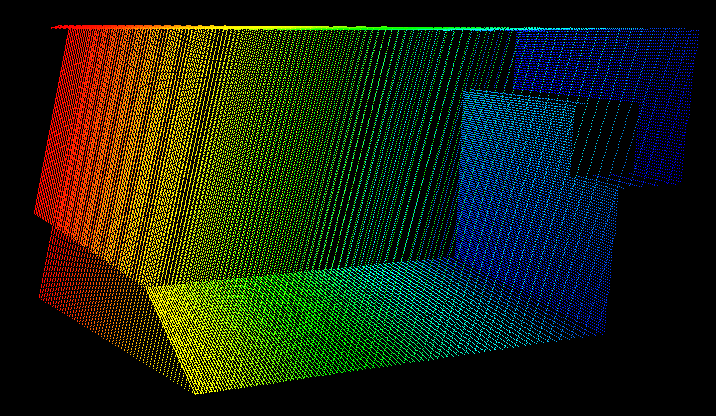
The full gist is available here. It uses cubes as package shapes and can be set up for different geometries and camera properties.

I also used it to get familiar with new C++11 features. I was pleasantly surprised. In all, the C++ version was only about 15% more lines of code than the Ruby version I started prototyping. And the C++ version generates a whole load profile much faster than I can generate just one point cloud in Ruby. PCL doesn’t seem to play nice with C++11 (at least, not when I include <limits> using Clang on my Mac), so I’m writing the PCD files manually. The only dependency is Eigen.